Einstein uses the postulates of special relativity and other known laws of physics to show the following:
Proposition. (Mass-energy equivalence) If a body at rest emits a total energy of E while remaining at rest, then the mass of that body decreases by  .
.
Assuming that bodies at rest with zero mass necessarily have zero energy, this implies the famous formula  – but only for bodies which are at rest. For moving bodies, there is a similar formula, but one has to first decide what the correct definition of mass is for moving bodies; I will not discuss this issue here, but see for instance the Wikipedia entry on this topic.
– but only for bodies which are at rest. For moving bodies, there is a similar formula, but one has to first decide what the correct definition of mass is for moving bodies; I will not discuss this issue here, but see for instance the Wikipedia entry on this topic.
Broadly speaking, the derivation of the above proposition proceeds via the following five steps:
- Using the postulates of special relativity, determine how space and time coordinates transform under changes of reference frame (i.e. derive theLorentz transformations).
- Using 1., determine how the temporal frequency
 (and wave number k) ofphotons transform under changes of reference frame (i.e. derive the formulae for relativistic Doppler shift).
(and wave number k) ofphotons transform under changes of reference frame (i.e. derive the formulae for relativistic Doppler shift).
- Using Planck’s law
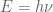 (and de Broglie’s law
(and de Broglie’s law  ) and 2., determine how the energy E (and momentum p) of photons transform under changes of reference frame.
) and 2., determine how the energy E (and momentum p) of photons transform under changes of reference frame.
- Using the law of conservation of energy (and momentum) and 3., determine how the energy (and momentum) of bodies transform under changes of reference frame.
- Comparing the results of 4. with the classical Newtonian approximations
 (and
(and  ), deduce the relativistic relationship between mass and energy for bodies at rest (and more generally between mass, velocity, energy, and momentum for moving bodies).
), deduce the relativistic relationship between mass and energy for bodies at rest (and more generally between mass, velocity, energy, and momentum for moving bodies).
Actually, as it turns out, Einstein’s analysis for bodies at rest only needs to understand changes of reference frame at infinitesimally low velocity, 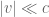 . However, in order to see enough relativistic effects to deduce the mass-energy equivalence, one needs to obtain formulae which are accurate to second order in v (or more precisely,
. However, in order to see enough relativistic effects to deduce the mass-energy equivalence, one needs to obtain formulae which are accurate to second order in v (or more precisely, 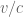 ), as opposed to those in Newtonian physics which are accurate to first order in v. Also, to understand the relationship between mass, velocity, energy, and momentum for moving bodies rather than bodies at rest, one needs to consider non-infinitesimal changes of reference frame.
), as opposed to those in Newtonian physics which are accurate to first order in v. Also, to understand the relationship between mass, velocity, energy, and momentum for moving bodies rather than bodies at rest, one needs to consider non-infinitesimal changes of reference frame.
Important note: Einstein’s argument is, of course, a physical argument rather than a mathematical one. While I will use the language and formalism of pure mathematics here, it should be emphasised that I am not exactly giving a formal proof of the above Proposition in the sense of modern mathematics; these arguments are instead more like the classical proofs of Euclid, in that numerous “self evident” assumptions about space, time, velocity, etc. will be made along the way. (Indeed, there is a very strong analogy between Euclidean geometry and the Minkowskian geometry of special relativity.) One can of course make these assumptions more explicit, and this has been done in many other places, but I will avoid doing so here in order not to overly obscure Einstein’s original argument.
– Lorentz transforms to first order –
To simplify the notation, we shall assume that the ambient spacetime S has only one spatial dimension rather than three, although the analysis here works perfectly well in three spatial dimensions (as was done in Einstein’s original paper). Thus, in any inertial reference frame F, the spacetime S is parameterised by two real numbers (t,x). Mathematically, we can describe each frame F as a bijection between S and  . To normalise these coordinates, let us suppose that all reference frames agree to use a single event O in S as their origin (0,0); thus
. To normalise these coordinates, let us suppose that all reference frames agree to use a single event O in S as their origin (0,0); thus
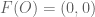 (1)
(1)
for all frames F.
Given an inertial reference frame 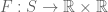 , one can generate new inertial reference frames in two different ways. One is by reflection: one takes the same frame, with the same time coordinate, but reverses the space coordinates to obtain a new frame
, one can generate new inertial reference frames in two different ways. One is by reflection: one takes the same frame, with the same time coordinate, but reverses the space coordinates to obtain a new frame 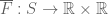 , thus reversing the orientation of the frame. In equations, we have
, thus reversing the orientation of the frame. In equations, we have
if  , then
, then  (2)
(2)
for any spacetime event E. Another way is by replacing the observer which is stationary in F with an observer which is moving at a constant velocity v in F, to create a new inertial reference frame  with the same orientation as F. In our analysis, we will only need to understand infinitesimally small velocities v; there will be no need to consider observers traveling at speeds close to the speed of light.
with the same orientation as F. In our analysis, we will only need to understand infinitesimally small velocities v; there will be no need to consider observers traveling at speeds close to the speed of light.
The new frame  and the original frame
and the original frame 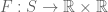 must be related by some transformation law
must be related by some transformation law
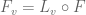 (3)
(3)
for some bijection  . A priori, this bijection
. A priori, this bijection 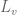 could depend on the original frame F as well as on the velocity v, but the principle of relativity implies that
could depend on the original frame F as well as on the velocity v, but the principle of relativity implies that 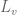 is in fact the same in all reference frames F, and so only depends on v.
is in fact the same in all reference frames F, and so only depends on v.
It is thus of interest to determine what the bijections  are. From our normalisation (1) we have
are. From our normalisation (1) we have
 (4)
(4)
but this is of course not enough information to fully specify 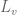 . To proceed further, we recall Newton’s first law, which states that an object with no external forces applied to it moves at constant velocity, and thus traverses a straight line in spacetime as measured in any inertial reference frame. (We are assuming here that the property of “having no external forces applied to it” is not affected by changes of inertial reference frame. For non-inertial reference frames, the situation is more complicated due to the appearance of fictitious forces.) This implies that
. To proceed further, we recall Newton’s first law, which states that an object with no external forces applied to it moves at constant velocity, and thus traverses a straight line in spacetime as measured in any inertial reference frame. (We are assuming here that the property of “having no external forces applied to it” is not affected by changes of inertial reference frame. For non-inertial reference frames, the situation is more complicated due to the appearance of fictitious forces.) This implies that 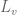 transforms straight lines to straight lines. (To be pedantic, we have only shown this for straight lines corresponding to velocities that are physically attainable, but let us ignore this minor technicality here.) Combining this with (4), we conclude that
transforms straight lines to straight lines. (To be pedantic, we have only shown this for straight lines corresponding to velocities that are physically attainable, but let us ignore this minor technicality here.) Combining this with (4), we conclude that 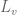 is a linear transformation. (It is a cute exercise to verify this claim formally, under reasonable assumptions such as smoothness of
is a linear transformation. (It is a cute exercise to verify this claim formally, under reasonable assumptions such as smoothness of 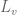 . ) Thus we can view
. ) Thus we can view 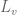 now as a
now as a  matrix.
matrix.
When v=0, it is clear that 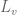 should be the identity matrix I. Making the plausible assumption that
should be the identity matrix I. Making the plausible assumption that 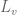 varies smoothly with v, we thus have the Taylor expansion
varies smoothly with v, we thus have the Taylor expansion
 (5)
(5)
for some matrix 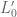 and for infinitesimally small velocities v. (Mathematically, what we are doing here is analysing the Lie group of transformations
and for infinitesimally small velocities v. (Mathematically, what we are doing here is analysing the Lie group of transformations 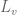 via itsLie algebra.) Expanding everything out in coordinates, we obtain
via itsLie algebra.) Expanding everything out in coordinates, we obtain

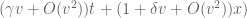 (6)
(6)
for some absolute constants 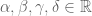 (not depending on t, x, or v).
(not depending on t, x, or v).
The next step, of course, is to pin down what these four constants are. We can use the reflection symmetry (2) to eliminate two of these constants. Indeed, if an observer is moving at velocity v in frame F, it is moving in velocity -v in frame  , and hence
, and hence  . Combining this with (2), (3), (6) one eventually obtains
. Combining this with (2), (3), (6) one eventually obtains
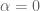 and
and 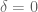 . (7)
. (7)
Next, if a particle moves at velocity v in frame F, and more specifically moves along the worldline 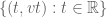 , then it will be at rest in frame
, then it will be at rest in frame 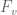 , and (since it passes through the universally agreed upon origin O) must then lie on the worldline
, and (since it passes through the universally agreed upon origin O) must then lie on the worldline 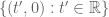 . From (3), we conclude
. From (3), we conclude
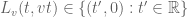 for all t. (8)
for all t. (8)
Inserting this into (6) (and using (7)) we conclude that 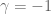 . We have thus pinned down
. We have thus pinned down 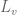 to first order almost completely:
to first order almost completely:
 (9)
(9)
Thus, rather remarkably, using nothing more than the principle of relativity and Newton’s first law, we have almost entirely determined the reference frame transformation laws, save for the question of determining the real number  . [In mathematical terms, what we have done is classify the one-dimensional Lie subalgebras of
. [In mathematical terms, what we have done is classify the one-dimensional Lie subalgebras of 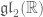 which are invariant under spatial reflection, and coordinatised using (8).] If this number vanished, we would eventually recover classical Galilean relativity. If this number was positive, we would eventually end up with the (rather unphysical) situation of Euclidean relativity, in which spacetime had a geometry isomorphic to that of the Euclidean plane. As it turns out, though, in special relativity this number is negative. This follows from the second postulate of special relativity, which asserts that the speed of light c is the same in all inertial reference frames. In equations (and because
which are invariant under spatial reflection, and coordinatised using (8).] If this number vanished, we would eventually recover classical Galilean relativity. If this number was positive, we would eventually end up with the (rather unphysical) situation of Euclidean relativity, in which spacetime had a geometry isomorphic to that of the Euclidean plane. As it turns out, though, in special relativity this number is negative. This follows from the second postulate of special relativity, which asserts that the speed of light c is the same in all inertial reference frames. In equations (and because 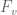 has the same orientation as F), this is asserting that
has the same orientation as F), this is asserting that
 for all t (10+)
for all t (10+)
and
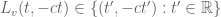 for all t. (10-)
for all t. (10-)
Inserting either of (10+) or (10-) into (9) we conclude that  , and thus we have obtained a full description of
, and thus we have obtained a full description of 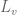 to first order:
to first order:
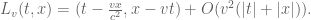 (11)
(11)
— Lorentz transforms to second order –
It turns out that to get the mass-energy equivalence, first-order expansion of the Lorentz transformations 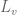 is not sufficient; we need to expand to second order. From Taylor expansion we know that
is not sufficient; we need to expand to second order. From Taylor expansion we know that
 (12)
(12)
for some matrix 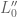 . To compute this matrix, let us make the plausible assumption that if the frame
. To compute this matrix, let us make the plausible assumption that if the frame 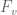 is moving at velocity v with respect to F, then F is moving at velocity -v with respect to
is moving at velocity v with respect to F, then F is moving at velocity -v with respect to 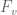 . (One can justify this by considering two frames receding at equal and opposite directions from a single reference frame, and using reflection symmetry to consider how these two frames move with respect to each other.) Applying (3) we conclude that
. (One can justify this by considering two frames receding at equal and opposite directions from a single reference frame, and using reflection symmetry to consider how these two frames move with respect to each other.) Applying (3) we conclude that 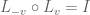 . Inserting this into (12) and comparing coefficients we conclude that
. Inserting this into (12) and comparing coefficients we conclude that 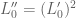 . Since
. Since 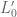 is determined from (11), we can compute everything explicitly, eventually ending up at the second order expansion
is determined from (11), we can compute everything explicitly, eventually ending up at the second order expansion
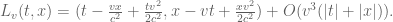 (13)
(13)
One can continue in this fashion (exploiting the fact that the 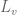 must form a Lie group (with the Lie algebra already determined), and using (8) to fix the parameterisation
must form a Lie group (with the Lie algebra already determined), and using (8) to fix the parameterisation 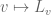 of that group) to eventually get the full expansion of
of that group) to eventually get the full expansion of 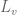 , namely
, namely
 ,
,
but we will not need to do so here.
— Doppler shift –
The formula (13) is already enough to recover the relativistic Doppler shiftformula (to second order in v) for radiation moving at speed c with some wave number k. Mathematically, such radiation moving to the right in an inertial reference frame F can be modeled by the function

for some amplitude A and phase shift 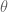 . If we move to the coordinates
. If we move to the coordinates 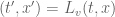 provided by an inertial reference frame F’, a computation then shows that the function becomes
provided by an inertial reference frame F’, a computation then shows that the function becomes
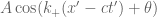
where 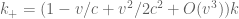 . (actually, if the radiation is tensor-valued, the amplitude A might also transform in some manner, but this transformation will not be of relevance to us.) Similarly, radiation moving at speed c to the left will transform from
. (actually, if the radiation is tensor-valued, the amplitude A might also transform in some manner, but this transformation will not be of relevance to us.) Similarly, radiation moving at speed c to the left will transform from

to
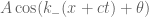
where  . This describes how the wave number k transforms under changes of reference frame by small velocities v. The temporal frequency
. This describes how the wave number k transforms under changes of reference frame by small velocities v. The temporal frequency  is linearly related to the wave number k by the formula
is linearly related to the wave number k by the formula
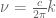 , (14)
, (14)
and so this frequency transforms by the (
red-shift) formula
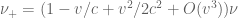 (15+)
(15+)
for right-ward moving radiation and by the (blue-shift) formula
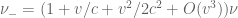 (15-)
(15-)
for left-ward moving radiation. (As before, one can give an exact formula here, but the above asymptotic will suffice for us.)
– Energy and momentum of photons –
From the work of Planck, and of Einstein himself on the photoelectric effect, it was known that light could be viewed both as a form of radiation (moving at speed c), and also made up of particles (photons). From Planck’s law, each photon has an energy of  and (from de Broglie’s law) a momentum of
and (from de Broglie’s law) a momentum of  , where h is Planck’s constant, and the sign depends on whether one is moving rightward or leftward. In particular, from (14) we have the pleasant relationship
, where h is Planck’s constant, and the sign depends on whether one is moving rightward or leftward. In particular, from (14) we have the pleasant relationship
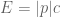 (16)
(16)
for photons. [More generally, it turns out that for arbitrary bodies, momentum, velocity, and energy are related by the formula  , though we will not derive this fact here.] Applying (15+), (15-), we see that if we view a photon in a new reference frame
, though we will not derive this fact here.] Applying (15+), (15-), we see that if we view a photon in a new reference frame 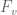 , then the observed energy E and momentum p now become
, then the observed energy E and momentum p now become
 ;
;  (17+)
(17+)
for right-ward moving photons, and
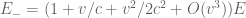 ;
;  (17-)
(17-)
for left-ward moving photons.
These two formulae (17+), (17-) can be unified using (16) into a single formula
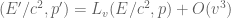 (18)
(18)
for any photon (moving either leftward or rightward) with energy E and momentum p as measured in frame F, and energy E’ and momentum p’ as measured in frame 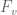 . Actually, the error term
. Actually, the error term 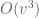 can be deleted entirely by working a little harder. From the linearity of
can be deleted entirely by working a little harder. From the linearity of 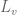 and the conservation of energy and momentum, it is then natural to conclude that (18) should also be valid not only for photons, but for any object that can exchange energy and momentum with photons. This can be used to derive the formula
and the conservation of energy and momentum, it is then natural to conclude that (18) should also be valid not only for photons, but for any object that can exchange energy and momentum with photons. This can be used to derive the formula  fairly quickly, but let us instead give the original argument of Einstein, which is only slightly different.
fairly quickly, but let us instead give the original argument of Einstein, which is only slightly different.
— Einstein’s argument –
We are now ready to give Einstein’s argument. Consider a body at rest in a reference frame F with some mass  and some rest energy
and some rest energy 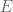 . (We do not yet know that
. (We do not yet know that 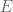 is equal to
is equal to 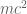 .) Now let us view this same mass in some new reference frame
.) Now let us view this same mass in some new reference frame 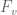 , where v is a small velocity. From Newtonian mechanics, we know that a body of mass
, where v is a small velocity. From Newtonian mechanics, we know that a body of mass  moving at velocity v acquires a kinetic energy of
moving at velocity v acquires a kinetic energy of 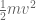 . Thus, assuming that Newtonian physics is valid at low velocities to top order, the net energy E’ of this body as viewed in this frame
. Thus, assuming that Newtonian physics is valid at low velocities to top order, the net energy E’ of this body as viewed in this frame 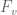 should be
should be
 (19)
(19)
If assumes that the transformation law (18) applies for this body, one can already deduce the formula  for this body at rest from (19) (and the assumption that bodies at rest have zero momentum), but let us instead give Einstein’s original argument.
for this body at rest from (19) (and the assumption that bodies at rest have zero momentum), but let us instead give Einstein’s original argument.
We return to frame F, and assume that our body emits two photons of equal energy  , one moving left-ward and one moving right-ward. By (16) and conservation of momentum, we see that the body remains at rest after this emission. By conservation of energy, the remaining energy in the body is
, one moving left-ward and one moving right-ward. By (16) and conservation of momentum, we see that the body remains at rest after this emission. By conservation of energy, the remaining energy in the body is 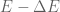 . Let’s say that the new mass in the body is
. Let’s say that the new mass in the body is  . Our task is to show that
. Our task is to show that  .
.
To do this, we return to frame 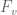 . By (16+), the rightward moving photon has energy
. By (16+), the rightward moving photon has energy
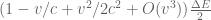 ; (20+)
; (20+)
in this frame; similarly, the leftward moving photon has energy
 . (20-)
. (20-)
What about the body? By repeating the derivation of (18), it must have energy
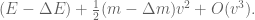 (20)
(20)
By the principle of relativity, the law of conservation of energy has to hold in the frame 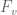 as well as in the frame F. Thus, the energy (20-)+(20+)+(20) in frame
as well as in the frame F. Thus, the energy (20-)+(20+)+(20) in frame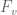 after the emission must equal the energy E’=(19) in frame
after the emission must equal the energy E’=(19) in frame 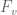 before emission. Adding everything together and comparing coefficients we obtain the desired relationship
before emission. Adding everything together and comparing coefficients we obtain the desired relationship  .
.
[One might quibble that Einstein’s argument only applies to emissions of energy that consist of equal and opposite pairs of photons. But one can easily generalise the argument to handle arbitrary photon emissions, especially if one takes advantage of (18); for instance, another well-known (and somewhat simpler) variant of the argument works by considering a photon emitted from one side of a box and absorbed on the other. More generally, any other energy emission which could potentially in the future decompose entirely into photons would also be handled by this argument, thanks to conservation of energy. Now, it is possible that other conservation laws prevent decomposition into photons; for instance, the law of conservation of charge prevents an electron (say) from decomposing entirely into photons, thus leaving open the possibility of having to add a linearly charge-dependent correction term to the formula  . But then one can renormalise away this term by redefining the energy to subtract such a term; note that this does not affect conservation of energy, thanks to conservation of charge.]
. But then one can renormalise away this term by redefining the energy to subtract such a term; note that this does not affect conservation of energy, thanks to conservation of charge.]
82 comments