[Submitted on 11 Mar 1998]
Massive 3-loop Feynman diagrams reducible to SC* primitives of algebras of the sixth root of unity
In each of the 10 cases with propagators of unit or zero mass, the finite part of the scalar 3-loop tetrahedral vacuum diagram is reduced to 4-letter words in the 7-letter alphabet of the 1-forms Ω:=dz/z and ωp:=dz/(λ−p−z), where λ is the sixth root of unity. Three diagrams yield only ζ(Ω3ω0)=1/90π4. In two cases π4 combines with the Euler-Zagier sum ζ(Ω2ω3ω0)=∑m>n>0(−1)m+n/m3n; in three cases it combines with the square of Clausen’s Cl2(π/3)=Iζ(Ωω1)=∑n>0sin(πn/3)/n2. The case with 6 masses involves no further constant; with 5 masses a Deligne-Euler-Zagier sum appears: Rζ(Ω2ω3ω1)=∑m>n>0(−1)mcos(2πn/3)/m3n. The previously unidentified term in the 3-loop rho-parameter of the standard model is merely D3=6ζ(3)−6Cl22(π/3)−1/24π4. The remarkable simplicity of these results stems from two shuffle algebras: one for nested sums; the other for iterated integrals. Each diagram evaluates to 10 000 digits in seconds, because the primitive words are transformable to exponentially convergent single sums, as recently shown for ζ(3) and ζ(5), familiar in QCD. Those are SC∗(2) constants, whose base of super-fast computation is 2. Mass involves the novel base-3 set SC∗(3). All 10 diagrams reduce to SC∗(3)∪SC∗(2) constants and their products. Only the 6-mass case entails both bases.
| Comments: | 41 pages, LaTeX |
| Subjects: | High Energy Physics – Theory (hep-th); High Energy Physics – Phenomenology (hep-ph); Classical Analysis and ODEs (math.CA) |
| Journal reference: | Eur.Phys.J.C8:311-333,1999 |
| DOI: | 10.1007/s100529900935 |
| Report number: | OUT–4102–72 |
| Cite as: | arXiv:hep-th/9803091 |
| (or arXiv:hep-th/9803091v1 for this version) |
Figure Eight Knot
https://mathworld.wolfram.com/FigureEightKnot.html

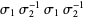
The figure eight knot, also known as the Flemish knot and savoy knot, is the unique prime knot of four crossings 04-001. It has braid word .
The figure eight knot is implemented in the Wolfram Language as KnotData[“FigureEight”].
It is a 2-embeddable knot, and is amphichiral as well as invertible. It has Arf invariant 1. It is not a slice knot (Rolfsen 1976, p. 224).
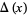
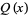
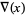
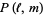
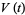
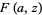
The Alexander polynomial , BLM/Ho polynomial , Conway polynomial , HOMFLY polynomial , Jones polynomial , and Kauffman polynomial F of the figure eight knot are
| (1) | |||
| (2) | |||
| (3) | |||
| (4) | |||
| (5) | |||
| (6) |
There are no other knots on 10 or fewer crossings sharing the same Alexander polynomial, BLM/Ho polynomial, bracket polynomial, HOMFLY polynomial, Jones polynomial, or Kauffman polynomial F.
The figure eight knot has knot group
| (7) |
(Rolfsen 1976, p. 58).

Helaman Ferguson’s sculpture “Figure-Eight Complement II” illustrates the knot complement of the figure eight knot (Borwein and Bailey 2003, pp. 54-55, color plate IV, and front cover; Bailey et al. 2007, p. 37). Furthermore, Ferguson has carved the BBP-type formula for the hyperbolic volume of the knot complement (discussed below) on both figure eight knot complement sculptures commissioned by the Clay Mathematics Institute (Borwein and Bailey 2003, p. 56; Bailey et al. 2007, pp. 36-38).
The hyperbolic volume of the knot complement of the figure eight knot is approximately given by
| (8) |
(OEIS A091518). Exact expressions are given by the infinite sums
| (9) | |||
| (10) | |||
| (11) | |||
| (12) | |||
| (13) |
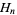
where is a harmonic number.
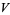
has a variety of BBP-type formulas including
| (14) | |||
| (15) | |||
| (16) | |||
| (17) | |||
| (18) |
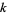
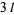
with additional identities for coefficients of of the form (E. W. Weisstein, Sep. 30, 2007). Higher-order identities are
| (19) |
(E. W. Weisstein, Aug. 11, 2008).
Additional classes of identities are given by
| (20) | |||
| (21) |
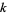
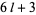
with additional identities for coefficients of of the form (E. W. Weisstein, Sep. 30, 2007). Another BBP-type formula is given by
| (22) |
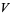
is also given by the integrals
| (23) | |||
| (24) | |||
| (25) |
and the analytic expressions
| (26) | |||
| (27) | |||
| (28) | |||
| (29) | |||
| (30) | |||
| (31) | |||
| (32) | |||
| (33) |
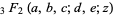
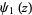
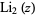
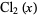
(Broadhurst 1998; Borwein and Bailey 2003, pp. 54 and 88-92; Bailey et al. 2007, pp. 36-38 and 265-266), where is a generalized hypergeometric function, is the trigamma function, is the dilogarithm and is Clausen’s integral.SEE ALSO:BBP-Type Formula, Knot, Prime KnotREFERENCES:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Bar-Natan, D. “The Knot .” https://www.math.toronto.edu/~drorbn/KAtlas/Knots/4.1.html.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Broadhurst, D. J. “Massive 3-Loop Feynman Diagrams Reducible to Primitives of Algebras of the Sixth Root of Unity.” March 11, 1998. https://arxiv.org/abs/hep-th/9803091.
Francis, G. K. A Topological Picture Book. New York: Springer-Verlag, 1987.
Kauffman, L. Knots and Physics. Teaneck, NJ: World Scientific, pp. 8, 12, and 35, 1991.
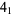
KnotPlot. “.” https://newweb.cecm.sfu.ca/cgi-bin/KnotPlot/KnotServer/kserver?ncomp=1&ncross=4&id=1.
Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., pp. 21 and 153, 1993.
Owen, P. Knots. Philadelphia, PA: Courage, p. 16, 1993.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 58 and 224, 1976.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. Middlesex, England: Penguin Books, pp. 78-79, 1991.CITE THIS AS:
Weisstein, Eric W. “Figure Eight Knot.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/FigureEightKnot.html
https://www.researchgate.net/publication/41654906_Biophysics_of_Knotting#pf3
350 Meluzzi·Smith·Arya
Annu. Rev. Biophys. 2010.39:349-366. Downloaded from arjournals.annualreviews.org by University of California – San Diego on 05/31/10. For personal use only.
a
c
b
51
52
31 Trefoil
41 Figure-eight
Closed curve Open curve
Projection
g
SK
SK
SP
SP
SK D
e
d
f Square knot
Granny knot
Slipknot
q–1 + q–3 – q–4
q2 – q + 1 –q–1 + q–2
q–2 + q–4 – q–5 + q–6 – q–7
q–1 – q–2 + 2q–3 – q–4 + q–5 – q–6
SK
a
Figure 1 Knot types and features. (a) Knots formally exist only in 3D curves (left). Knot projections are 2D representations of knots (right). (b) Knot-like conformations in open curves are often encountered in biophysics (left). To analyze such knots, their loose ends must be connected, according to some procedure, to obtainaclosedcurve(right).(c)Projectionsofthefoursimplestnontrivialknottypes,withthecorresponding CS denominations and Jones polynomials (see text for definition of CS) (adapted from http://katlas.math. toronto.edu/wiki/Main Page). (d) The size of a knot, SK, in a polymer may be less than the size of the polymer, SP, containing the knot. (e) In a slip link arrangement, entropic competition between the knotted loops causes the ring to squeeze one of the knots. The size of the latter can be deduced from the position of the ring. Adapted from Reference 64. (f ) The size of a tight knot can be estimated from the volume of the enclosing ideal knot representation: SK ∼(D2L)1/3, where D and L are the diameter and length of the outer tube. Adapted from Reference 39. (g) Square and granny knots can tie
file:///C:/Users/Dad/Downloads/paper20%20(1).pdf